Linear Regression Using Gradient Descent Python

Simple Linear regression

Simple Linear regression is one of the simplest and is going to be first AI algorithm which you will learn in this blog.

In statistics, a simple linear regression is a linear regression model with a single defining variable. That is, it relates to two-dimensional sample points with an independent variable and a dependent variable (traditionally, x and y coordinates in the Cartesian coordinate system) and finds a linear function (a non-vertical straight line), which As accurately as possible, predicts dependent variable values as an independent variable function. Simple adjective means that the variable of results is related to a single predictor.

Equation for simple linear function is

y = mx+c

where y is dependent variable which we want to predict and x is dependent variable,

I am trying to explain as much simple as possible, there are some other factors and techniques involved which I will discuss in next AI/Datascience blog.

As described earlier linear regression is a linear approach to modelling the relationship between a dependent variable and one or more independent variables. Let x be the independent variable and y be the dependent variable

This equation is used for single variable linear regression. This means we have two variables and we can plot data in 2D space.

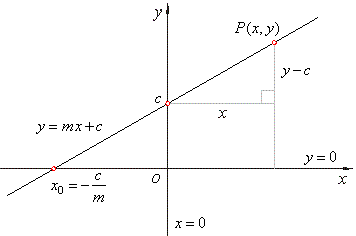
I will use an example of predicting salary based on Rank/Level.

So in this case, y in equation will be salary which we want to predict and x will be our level.

Lets plot the dataset,

Now we want our model to find perfect slope and y intercept by reducing the error, What I mean is that we have to fit a perfect line that touches as many data points as possible and has less error. Example is shown below

To minimize Loss, Loss function will be used.

Loss Function

The loss is the error in our predicted value of m and c. Our goal is to minimize this error to obtain the most accurate value of m and c.
We will use the Mean Squared Error function to calculate the loss. There are three steps in this function:

        1. Find the difference between the actual y and predicted y value(y = mx + c), for a given x.

        2. Square this difference.

        3. Find the mean of the squares for every value in X.

 

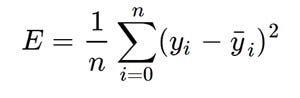
Mean Squared Error Equation

Here yᵢ is the actual value and ȳᵢ is the predicted value. Lets substitute the value of ȳᵢ:

 

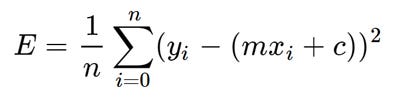
Substituting the value of ȳᵢ

So we square the error and find the mean. hence the name Mean Squared Error. Now that we have defined the loss function, lets see how to minimize loss by optimizing values of m and c.

Gradient Descent Algorithm

We will use this function to find optimized values for m & c

Gradient Descent is a local order iteration optimization algorithm in which at least one different local function is searched. The idea is to take repeated steps in the opposite direction to the inclination (or approximate inclination) of the function at the current point, as this is the direction of the fastest descent. In contrast, stepping in the direction of Milan will take this function to a more local level. This process is then called inclination.

Inshort we have to find local minima, which can be seen in graph below

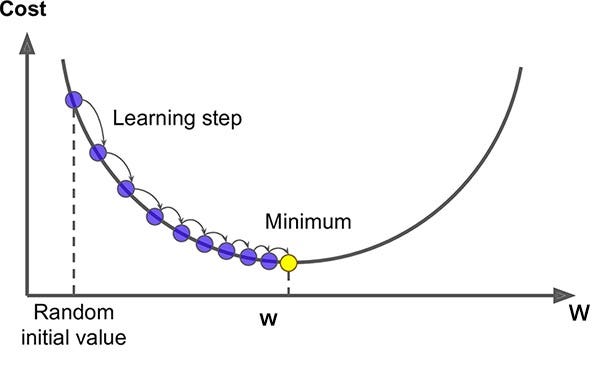
In 3D, It can be visualized as where B is our local minima point

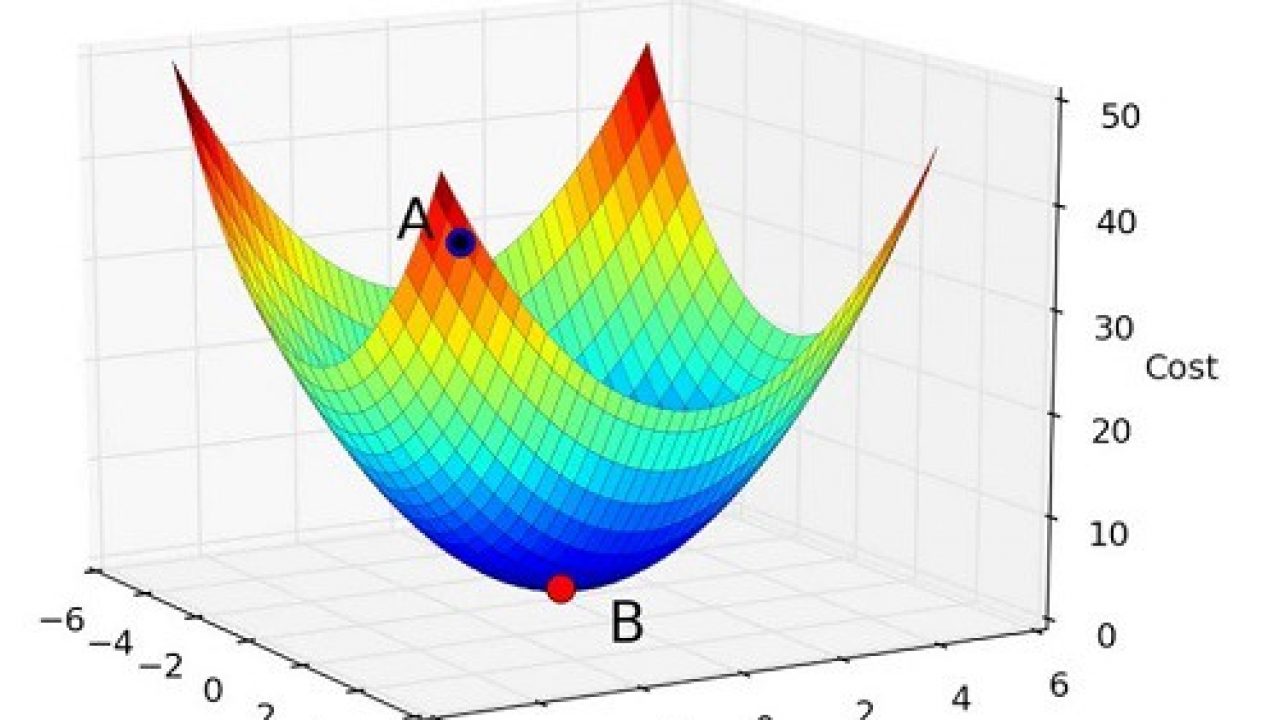
Let’s try applying gradient descent to m and c and approach it step by step:

1. Initially let m = 0 and c = 0. Let L be our learning rate. This controls how much the value of m changes with each step. L could be a small value like 0.0001 for good accuracy.

2. Calculate the partial derivative of the loss function with reference to m, and plug in the existing values of x, y, m and c to get the derivative value D.

 

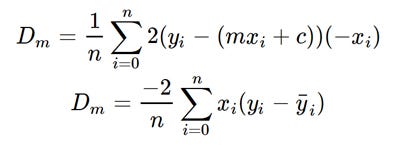
Derivative with respect to m

Dₘ is the value of the partial derivative with respect to m. Similarly lets find the partial derivative with respect to c, Dc :

 

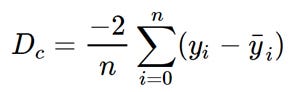
Derivative with respect to c

3. Now we update the current value of m and c using the following equation:

 

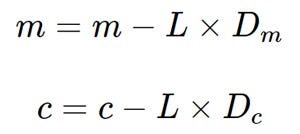
4. We repeat this process until our loss function is a very small value or ideally 0 (which means 0 error or 100% accuracy). The value of m and c that we are left with now will be the optimum values.

Now going back to our analogy, the current position of the person can be understood. D is equal to the steepness of the slope and L can be the speed at which it moves. Now the new value of m which we will calculate using the above equation will be its next position, and L-D will be the size of the steps it will take. When the shield is more steep (D is higher) it takes longer steps and when it is less steep (D is lower) it takes shorter steps. Eventually it reaches the bottom of the valley which is equal to our loss = 0.
Now our model is ready to predict with optimum value of m and c.

Code

def gradient_descent(x,y):
    n = len(x)
    
    m_current = 0 
    b_current = 0
    learning_rate = 0.0002
    iterations = 10000 #taking initially 1000 for test purpose
    previous_cost = 0
    for i in range(iterations):
        y_predicted = m_current * x + b_current
        cost_function = (1/n)*sum(y-y_predicted)
        cost_function = cost_function**2
        #cost = (1/n)*sum([value**2 for value in (y-y_predicted)])
        previous_cost = cost_function
        
        
        m_derivative = -(2/n)*sum(x*(y-y_predicted))
        b_derivative = -(2/n)*sum(y-y_predicted)
        
        m_current = m_current - learning_rate * m_derivative
        b_current = b_current - learning_rate * b_derivative
        #print(y_predicted)
        print(f'm_current = {m_current} b_current = {b_current} iteration # = {i} and cost = {cost_function}')
        #print(f'my cost = {cost_function}    orignal cost = {cost}')

 Pass Level as x and Salary as y in given code. and it will find optimized values of m and c.