
Decision tree algorithm is one of the most popular machine learning algorithms. It uses tree-like structures and their possible combinations to solve specific problems. It belongs to the category of supervised learning algorithms and can be used for classification and regression purposes.
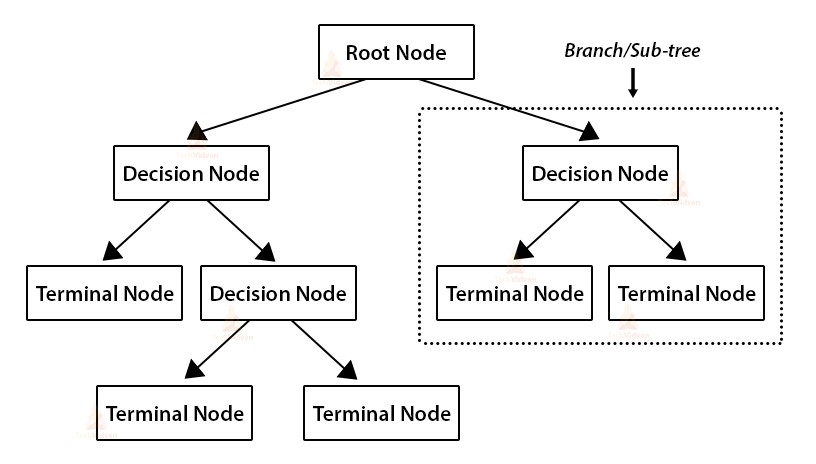
A decision tree is a structure that includes a root node, branches, and leaf nodes. Each inner node represents a test on an attribute, each branch represents the result of the test, and each leaf node contains a class label. The topmost node in the tree is the root node.
We made some assumptions when implementing the decision tree algorithm. These are listed below:-
1 - Initially, the entire training set is considered the root.
2 - The feature values need to be categorical. If the values are continuous, discretize them before building the model.
3 - Records are recursively distributed based on attribute values.
4 - The order in which attributes are placed as the root or internal nodes of the tree is done by using some statistical method.
In a decision tree algorithm, there is a tree-like structure where each internal node represents a test on an attribute, each branch represents the result of the test, and each leaf node represents a class label. The path from the root node to the leaf node represents the classification rule.We can see that there is some terminology involved in Decision Tree algorithm. The terms involved in Decision Tree algorithm are as follows:-
It represents the whole population or sample. It is further divided into two or more equal(homogeneous) sets.
It is a process of dividing a node into two or more sub-nodes (daughter nodes).
When a sub-node splits into further sub-nodes, then it is called a decision node.
Nodes that do not split further are called Leaf or Terminal nodes.
When we remove sub-nodes of a decision node, this process is called pruning. It is the opposite process of splitting.
A sub-section of an entire tree is called a branch or sub-tree.
A node, which is divided into sub-nodes is called the parent node of sub-nodes where sub-nodes are the children of a parent node.
The decision tree algorithm is one of the most commonly used and widely used supervised machine learning algorithms for both classification & regression tasks. The intuition behind the decision tree algorithm is easy to understand, as follows:-
1 - For each attribute in the dataset, the decision tree algorithm forms a node. The most important attributes are placed on the root node.
2 - To evaluate the task at hand, we start at the root node and work our way down the tree following the corresponding nodes that meet our conditions or decisions.
3 - This process continues until a leaf node is reached. It contains the prediction or outcome of a decision tree.
The main challenge for a decision tree implementation is to identify what we consider to be the root node and attributes at each level. This process is called attribute selection. There are different attribute selection metrics to identify attributes that can be considered the root node of each level.
There are two popular attribute selection measures. They are as follows:-
When using information gain as a criterion, we assume that attributes are categorical, and for the Gini index, attributes are assumed to be continuous.
Gini index, also known as Gini impurity, calculates the amount of probability that a particular feature will be misclassified when randomly selected. If all elements are linked with a class then it can be called pure class.
Let us understand the criterion of Gini index, like the nature of entropy, the Gini index varies between 0 and 1, where 0 represents the purity of the classification, i.e. all elements belong to a specified class or only one class exists. 1 means random distribution of elements across classes. A value of 0.5 for the Gini index indicates an even distribution of elements over some categories.
When designing a decision tree, the features with the smallest Gini index values will be given priority. You can learn another tree-based algorithm (random forest).
The Gini index is determined by subtracting the sum of squared probabilities for each category from one, and mathematically, the Gini index can be expressed as:
The concept of entropy plays an important role in calculating Information Gain.Information Gain is applied to quantify which feature provides maximal information about the classification based on the notion of entropy, i.e. by quantifying the size of uncertainty, disorder or impurity, in general, with the intention of decreasing the amount of entropy initiating from the top (root node) to bottom(leaves nodes).
The information gain takes the product of probabilities of the class with a log having base 2 of that class probability, the formula for Entropy is given below:
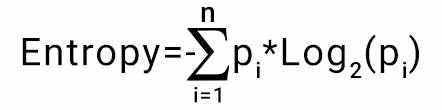
Here “p” denotes the probability that it is a function of entropy.
Entropy, In Lyman's words, it's not just a measure of disorder or purity. Basically, it's a measure of impurity or randomness in the data points.
Higher order disorder means low level impurities, let me simplify. Entropy is calculated between 0 and 1, although depending on the number of groups or classes present in the dataset, it may be greater than 1, but it means the same thing, a higher degree of disorder.
For the sake of explanation, let's limit the value of entropy to be between 0 and 1.
Overfitting is a significant practical difficulty for decision tree models and many other predictive models. Overfitting occurs when a learning algorithm continues to develop hypotheses to reduce the cost of training set errors
Increases the error on the test set. There are several ways to avoid overfitting when building decision trees.
1 - Pre-pruning of growing trees is stopped early until the training set is perfectly classified.
2 - Post-pruning allows the tree to classify the training set perfectly, then post-pruning the tree.
In practice, the second method of post-pruning the overfit tree is more successful because it is not easy to estimate exactly when to stop growing the tree.
An important step in tree pruning is to define a criterion for determining the correct final tree size using one of the following methods:
Use a different dataset in the training set (called the validation set) to evaluate the effect of pruned nodes in the tree.
Use the training set to build a tree, then apply statistical tests to estimate whether pruning or expanding specific nodes is likely to yield improvements over the training set.
Error estimation
Significance tests (such as chi-square tests)
Minimum description length principle: Using an explicit measure of the complexity of encoding the training set and decision tree, stop tree growth when the encoding size (size(tree) size(misclassifications(tree))) is minimized.
The first method is the most common method. In this approach, the available data is divided into two sets of examples: the training set used to build the decision tree and the validation set used to evaluate the impact of pruning the tree. The second method is also commonly used. Here, we explain error estimation and the Chi2 test.
from sklearn.datasets import load_iris from sklearn import tree iris = load_iris() X, y = iris.data, iris.target clf = tree.DecisionTreeClassifier() clf = clf.fit(X, y) #tree.plot_tree(clf) #uncomment to plot tree clf.predict(X) #2D data you want to predict